Saya mendapat kiriman pertanyaan dari seorang teman, bagaimana cara menghitung deviation standard (simpangan baku) untuk data kelompok?, lah saya bingung juga, sebelum-sebelumnya kalau ngitung simpangan baku selalu menggunakan data tunggal. Saya mencoba searching di google ternyata artikel yang berbahasa Indonesia masih sangat kurang. Saya menemukan dua website itupun hanya menampilkan rumusnya saja. Namun, ketika saya searching artikel berbahasa Inggris Masya Allah sangat banyak yang membahas cara menghitung simpangan baku untuk data berkelompok.
Berikut adalah contoh soal yang diperoleh dari data contoh (sample), kita akan mencoba menghitung rataan dan ragam (variance), dan simpangan baku.
No. | Inteval | Frekuensi |
1 | 41-45 | 2 |
2 | 46-50 | 5 |
3 | 51-55 | 10 |
4 | 56-60 | 6 |
5 | 61-65 | 2 |
Agar lebih mudah dihitung, kita dapat membuat tabel seperti berikut:
Rataan Sampel :
{\bar{x}=\frac{\sum_{i=1}^{5}f_{i}x_{i}}{n}=\frac{2\cdot 43+5\cdot 48+\cdot \cdot \cdot +2\cdot 63}{25}}
{\bar{x}=\frac{1330}{25}=53,2}
Ragam (Variansi) Sampel :
{s^{2}=\frac{\sum_{i=1}^{5}f_{i}(x_{i}-\bar{x})^{2}}{n-1}}
{s^{2}=\frac{2\cdot (43-53,2)^{2}+5\cdot (48-53,2)^{2}+\cdot \cdot \cdot +2\cdot (63-53,2)^{2}}{24}}
{s^{2}=\frac{797,21}{24}= 33,22}
Simpangan Baku Sampel :
{s=\sqrt{\frac{\sum_{i=1}^{5}f_{i}(x_{i}-\bar{x})^{2}}{n-1}}}
{s=\sqrt{33,22}=5,76}
Sumber: https://www.statistics-made-easy.com/variance-and-standard-deviation-for-grouped-data/








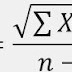








Itu yang rataan sampel, kayaknya salah deh. Untuk menghitung x bar (rat-rata) pembagianya adalag Fi/n (banyaknta frekuensi). Bukan n-1. Tapi kalau yang simpangan baku emang pembagiany n1
BalasHapusterima kasih sudah dikomentari mas Heri setyono, mas Heri benar pembaginya n untuk menghitung rata-rata. saya telah mengoreksinya.
HapusKomentar ini telah dihapus oleh pengarang.
BalasHapus