Mungkin kita sering menggunakan model regresi linear, model regresi eksponensial, dan masih banyak lagi. Seringkali kita bertanya, seberapa akurat model yang kita gunakan? Bagaimana mengeceknya? Mungkin bagi yang bergelut di dunia analisis statstik tidak asing lagi dengan istilah R Square (R2) atau biasa juga disebut sebagai koefisien determinasi.
R2 merupakan ukuran kekuatan prediksi.
R2 mencerminkan kecocokan antara model dan data.
R2 menentukan seberapa besar peubah X dapat menjelaskan peubah Y
Kisaran nilai R2 adalah 0 sampai 1, semakin besar nilai R2 maka semakin baik model tersebut untuk memprediksi peubah Y.
Contoh kasus (kasus ini hanya karangan saya agar mudah dipahami):
Saya telah memprediksi Hasil Penjualan (Y) Warung Coto Makassar di Wilayah Makasar dengan peubah Penjelas (X) adalah Luas Warung. Saya memperoleh nilai R2 = 35%, berarti sebanyak 35% peubah Luas Warung dapat menjelaskan/memberikan informasi untuk memprediksi hasil penjualan warung Coto Makassar.
Lalu bagaimana jika saya ingin menambah peubah penjelas pada kasus di atas? Apakah model prediksi saya tetap mendekati dengan data sebenarnya? Apakah R2 nya akan meningkat?
Kasus di atas merupakan kasus regresi linear sederhana. Lalu bagaimana jika saya menambah jumlah peubah penjelasnya, bukan satu peubah penjelas lagi tetapi kita akan menggunakan dua atau lebih peubah penjelas untuk memprediksi kasus di atas (hasil penjualan warung coto Makassar).
Misalkan setelah saya menambah peubah penjelas Lama Berdirinya Warung (X2) dan Luas Parkir (X3) untuk memprediksi Hasil Penjualan warung Coto. Sekarang peubah penjelasnya berapa? Ada tiga yah. Lalu saya peroleh hasil analisis dan ternyata nilai R2 = 35%.
Apakah ada perubahan nilai R2 setelah saya tambahkan peubah penjelas? jawabanya tidak. Mengapa? Karena R2 memiliki sifat hanya meningkat atau tetap konstan tetapi tidak pernah berkurang jika peubah penjelas ditambahkan ke dalam model. Teman-teman boleh menambah referensi bacaan terkait masalah ini https://www.analyticsvidhya.com . Jadi kalau teman-teman menemukan kasus R2 menjadi sangat besar atau konstan setelah ditambahkan peubah penjelas maka jangan dipercaya hasil tersebut karena itu merupakan kelemahan dari R2.
Lalu bagaimana?
Oleh karena kelemahan tersebut maka kita menggunakan "Adjusted R-Square".
The Adjusted R-Square adalah bentuk modifikasi dari R-Square yang telah disesuaikan jumlah peubah penjelas di dalam model. Jadi dengan menggunakan Adjusted R-Square, peubah penjelas telah terkoreksi.
Dimana:
R2 = Sample R square
p = Number of predictors
N = total sample size
Berikan Komentar Jika Bermanfaat dan jika ada Koreksi ^_^







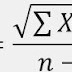








Tidak ada komentar:
Posting Komentar